A Novel Raytracing Algorithm for GPU

28 Jan 2014, 21:17 UTC

When I wrote a raytracer for Geomerics, I used all the Ingo Wald techniques I could understand. I made a nice kd-tree using the Surface Area Heuristic, fast triangle intersection code, and so on. But for a 20-level tree it is dismaying to see your algorithm descend 20 times, only to then go up and down a few times before striking a triangle. Most of the time is taken by descending & re-ascending the kd-tree.

There are ways around this for primary rays - descend to the leaf node containing the eye, and store the stack. Then "replay" this stack for each ray. This can be fast and efficient if you don't write to the stored stack so it can be reused for a million+ rays. But it doesn't easily work for secondary rays.

Then there is the issue of GPU raytracing. A stack? You have the luxury of a stack?!

While messing around creating WebGL demos last year, I stumbled on a technique with the following properties:

• Stackless traversal of space
• Leverages the GPU's special-purpose hardware (namely, the texture units)
• Has good cache coherence unless the rays are highly divergent

In other words, it's reasonably fast, at least on simple scenes. The disadvantage is, your acceleration structure is rather hard to build, and probably takes more space than a kd-tree.

The Basic Idea

The basic idea is to have leaves of your acceleration structure be cuboids (as they are in a kd-tree), except they have to have extents which are integers. Think of a unit-voxel subdivision on all of space, and each leaf is a cuboidal set of voxels. I'm going to call such a cuboid a "division" or "div".

Now, we give each div an index. The example code uses 16-bit indexes, for eventual inclusion in a DXGI_FORMAT_R16_UINT texture.

Next, we're going to paint the faces of the div with texture maps. These are usually going to be painted on the inside of the div. The texture maps are point-sampled, and aligned to voxel space so each texel represents a single face in the larger voxel space. In the texel we store the address of the adjacent div i.e. the div that a ray hitting that texel would enter next. If there is no adjacent div (e.g. the face is solid) we store a special value (e.g. zero).

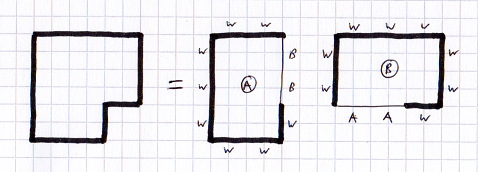
Here is a very simple 2D level split into two divs. The letters around each face show where that face goes to (W = wall, A,B = div A,B):

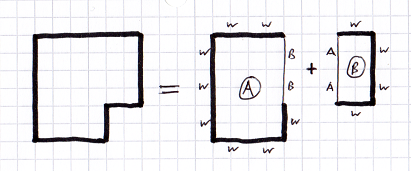
Now, to trace a ray we use the following steps. The only required state variable is the current div index:

1. Get the earliest intersection face on the div (the exit face) - this is done by calculating an intersection with +/-X, +/-Y and +/-Z and choosing the closest. Note that we only test one of +X or -X, depending on the ray's dX component.
2. Get the UV for that div face's texture map, and look up that texel.
3. Set the current div from the texel value.

This is highly numerically robust, as each intersection is done against a watertight eighth-space (the intersection of 3 half-spaces). We know when we enter a box that there will be some intersection. If the numbers are out slightly we just end up with slightly dodgy UVs, and a clamp operation can be used to bring these back to sane values. Essentially, the geometry of the situation dictates the paths and the numerical ray is only used to make decisions as to how to progress through that geometry. So long as the geometry is consistent, we shouldn't get holes or other artifacts.

Raytraced Wolf 3D

So, how do we use this to raytrace a Wolf 3D level? Well, in this case we will use half the texel values to mean various kinds of solid wall, and the other half to mean various adjacent divs. When we test the texel, if it's a solid wall, we stop iterating and use the texel data to find the correct material (e.g. one layer of a DX10 texture stack). We can use the subtexel UVs of the div intersection as the primary UVs for the material, sample that texture, and return the colour.

About the Screenshot

This is my DX11 code running at 718FPS on a GTX 280 at low resolution (720x360) with a lot of black space (no intersections)! The code has several inefficiencies.

Heuristics

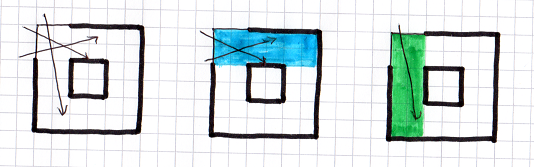
There are many ways to divide a Wolf 3D level into divs. A div represents a cuboid of empty space, so a division is like a rasterization of the empty space (except spans can be arbitrary rectangles, not just single-pixel strips). But rasterizations tend to have a principle axis, for instance:

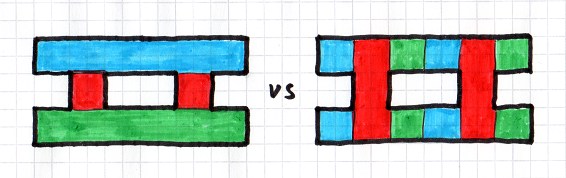
This principle axis can cause problems, since a ray going "against the grain" is going to have to traverse more divs.

The solution to this, which grows the tree data but makes the raytracer very fast, is that you don't have to pick a single rasterization of empty space. You can select elements from multiple rasterizations.

The problem then is to pick, for each possible voxel face, what is the best choice of div to use for rays entering that face.

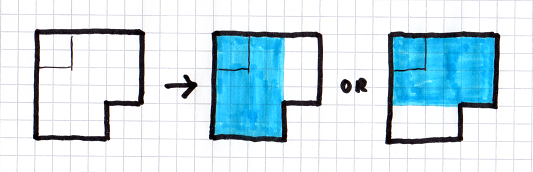
Note firstly that there is no point using a div which is a subset of a larger possible div. If we take for granted that for every voxel face there is some optimal choice of div, then there is nothing to gain by using a smaller div. Shared faces must have the same exit div, by uniqueness, and non-shared faces end up within the larger div, but cost another step to do so. Thus, we should always choose maximal divs which cannot be "grown" in any direction.

So, given a voxel face we're entering, we need to identify all the maximal divs which contain the voxel being entered:

Now, given that we know the rays are entering through a given voxel face, we can say something about the rays themselves. For instance, if the voxel face is at -X, then we know the rays all have dX > 0. So by raytracing a large set of candidate rays (over the surface of the entry face, and over the hemisphere dX > 0) we can see where they are likely to go next.

Now, we can use some heuristic, like making rays travel as far as possible before leaving the cell (and reducing the cost for rays which hit a wall, since they end here). Using this heuristic we choose which of the possible divs we want the rays to go into. (I don't know what the "best" heuristic is. The example code uses the expected length for all rays divided by the probability of hitting an exit face rather than a solid wall.)

Note that the rays are possibly confined to a sub-cuboid of the div we're considering, since we only consider maximal divs. For instance, in the image below, rays only enter a 1x2 cuboid, so we run our raytracing within that cuboid. But actually we're considering a 3x2 div. This makes no difference really, since rays cannot enter the extra 2x2 area, but we need to integrate over the correct volume and ignore the "unused" part of the div.

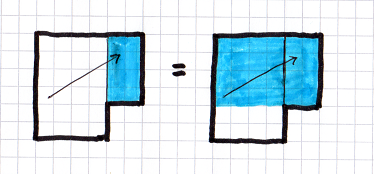
Note that this implies that rays can enter a div at any point in space, not just at a boundary face.

This is probably as clear as mud. Let's recap:

• All candidate divs are maximal (cannot be grown in any direction)
• The heuristic is evaluated over the cuboid the rays are actually entering
• The heuristic chooses which of the possible divs to use

For an example of this all at work, if we have the following arrangement of space, we will find that rays entering to the left of the top-left cell will enter a 3x1 space, but rays entering to the top of the top-left cell will enter a 1x3 space. In both cases, most rays then terminate, after only 1 step, and all rays terminate after 2 steps.

Compare this to a fixed rasterization, where some rays would travel through at least 3 steps. That is the power of using multiple rasterizations at the same time.

To finish, then, I lied about the example level. The example level actually looks like this:

(By the way, if you're worried about tracing thousands of test rays per div for the heuristic, don't. Start all test rays on the plane Z=0, with dZ > 0, and store how many rays go through each voxel face in all of space. These numbers can be used as a lookup table to determine the ray distribution over any cuboid. The function is symmetric in X and Y so only one octant of space needs to be stored. The example code encapsulates this data into the class FluxDensity, which is used by function IntegrateFluxDensityOverCuboid to calculate our heuristic over any cuboid in space.)

Storage

Storage is required for the textures painted onto each div, and for the div information itself.

The div textures are all stored in a texture atlas, which has format DXGI_FORMAT_R16_UINT.

The div info is stored using 8 texels of a DXGI_FORMAT_R8G8B8A8_UINT texture. Namely:

• Six texels are used to store U0,V0,U1,V1 for each face, which locates the div texture for that face within the atlas
• One texel stores SX,SY,SZ - the size of the div.
• One texel stores OX,OY,OZ - the location of the div in 3D space - plus a byte for div type.

Note that div type allows a div to be surfaced on the outside rather than on the inside. When raytracing a model, with an external eye, rather than a scene with an internal eye, an exterior div is used to direct rays entering the model to the appropriate interior div.

Div info units (8x1 texels) are packed into a larger 2D texture using a simple lexicographical ordering, as 1D textures have size limitations which are insufficient for our needs.

Shadows

I love raytracing because it avoids shadow maps, which I hate.

To get pixel-perfect shadows, find the nearest light (hey, maybe store this per cell) and fire a ray at it, from your intersection point. If you hit the light (this requires a new end-of-iteration test) then you are not in shadow; if you don't, then you are. Very straightforward.

The example code has separate loops for primary, shadow #1 and shadow #2 rays. Since the code is separate, it means the GPU has to run all the pixels through loop 1, then all the pixels through loop 2, etc. A better solution might be to compress all the code into one loop (the exact same StepRay function is used) and add code at the end to handle state transitions, in the style of an FSM. By paying careful attention to the FSM this could be made quite efficient, and would allow one pixel to still be tracing a primary ray while others were onto their shadow rays, etc.

Future Ideas

The above pretty much describes what I have. But the demo is a long way from a full game. I imagine when Carmack got to this stage with the original Wolf 3D he knew he was onto something, and they could proceed to developing a real game with it. But even so, there was other tech to construct - animated objects help, for a start!

Here are some ideas for future developments on this basic idea.

Recursion, Avoidance of

If we think about how shadow rays are cast now - in three seperate loops - but then think of compressing that down using an FSM, then we would be using an implicit stack. The FSM can perform "calls" one-deep to "functions" that either trace primary rays or shadow rays, simply by modifying & exchanging variables in a fixed way.

You can also do refraction in a similar way, provided you only trace the refracted ray and ignore the reflected ray (my demo here does this; in fact you have to trace the reflected ray instead when total internal reflection occurs, otherwise you get black holes in the render).

You can go further using accumulators and the like, to simulate blue glass or whatever (a colour filter) - so long as the ray never "forks" you're good.

And I recommend you keep it this way! Once you start "forking" rays you can use a stack up very quickly.

The only exception is, these walls are pretty boring. Wouldn't it be cool if I could have brickwork?

This can be done using a modified technique. When the rays enter a voxel face, they are transformed into a new space, and enter an instanced subspace where a brick wall lives. Thus, each brick wall is raytracing a copy of a generic brick wall a la texture mapping, but 3D.

However, if you miss the brick wall, you need to go back out into normal (non-instanced) space, and carry on where you left off, as if the brick wall wasn't there. This can be done if each instance can be made to live within a non-instanced "holding area". The walls of the holding area transport the rays back into normal space. The transformation for doing so could be built into the walls, somehow (i.e. stored in the div). Thus, you can do stateless transitions both into and out of instanced geometry, even if there are instances within instances, so long as you can store a small amount of extra data per instance.

Recursion, Non-avoidance of

So you can probably have a small stack on your GPU :)

You need a stack for correct translucency. This is because translucent layers have to be composited in the reverse order of being visited, so you need to stack all translucent intersection events, and then run that stack backwards to get pixel colour. I don't know, maybe there's a clever way to get around this.

You also need a stack for forking rays e.g. if you want to simulate physically-correct refraction, which includes both a refracted and a reflected ray.

I don't have much experience with OpenCL/DirectCompute/CUDA, but presumably you can use an unordered-access surface to implement a stack - cache the top entry in memory, fetch from the unordered-access surface after you pop, and maybe you won't stall until you try to pop again (?) To push, set the current top entry to memory and replace with the new entry. Hopefully writes won't stall the GPU either.

There may be a better way to do this, though. Does anyone with experience have any hints to give me? :)

LOD

LOD? In raytracing?

Well, yeah. Your main problem as your rays go further into space is that they diverge. Thus, every ray is eventually in a different cell, and cache coherency goes to hell.

Just like it does with non-mipped textures.

But, as with non-mipped textures, all this divergence gives you is noise - you're picking pixels from widely seperated areas of space, with no filtering of the stuff in between.

So let's mip-map space!

Each cell face can be mip-mapped, and the mip-map selected based on distance from ray origin or some other heuristic (for shadow rays, perhaps distance from ray origin of primary intersection + distance from primary intersection to shadow ray intersection). This does not use the "autoLOD" feature of GPUs, which hacks a screen-space derivative from a quad, but explicit LOD selection. (You should always use explicit LOD selection in your shaders, except when you need autoLOD, because autoLOD prevents some optimizations such as actual branches / early out.)

Now, when going through one of those faces we switch to a lower-res voxelization of all of space (each voxel face is a portal, and we're using that portal to go to another place, that's a lower-res version of this place). Now your rays are less divergent, because space is lower-res, so its cells are bigger.

Mip-mapped space may want to contain solid walls which are translucent, to emulate partial occupancy of a cell. This can be done the same way as other translucent surfaces, by accumulating a value as the ray travels. Does this make sense? Yes, because when you're in the mip-map world you're simulating the effect of tracing lots of rays which are close together at the origin (they all go through the same pixel) but not so close together in the current cell. If half those rays hit a wall and half do not, it's the same on average as if all the rays hit a wall with alpha = 1/2. So if you descend a mip level too soon, you'll get filtering over multiple pixels, which may not be what you want (hint: it isn't). But if you descend a mip at the "right" time then you are in effect simulating the effect of tracing multiple rays through the same pixel, and receiving an average result. This seems like it would be useful.

Since mip-mapped space uses the same coordinate system as regular space, but lower-resolution div textures (and larger divs) we can translate back from mip-mapped space to regular space if needed according to our mip-level heuristic. In other words, the top mip always goes back into full-resolution space, even within the mip world, to allow us to "escape" back out.

Things

A Wolf 3D game would be pretty boring without things in the rooms. How can we handle those?

Well, by using primitive intersection code you can calculate hit vs no-hit and everything else you need to shade the point and compute shadow rays etc.

But because of the way shaders are run, you'll either have all pixels in a group running this code or all pixels in a group tracing through space. So you'll lose some performance.

Worse, if you have two primitive types, the same phenomenon occurs, but with three sections of code - tracing, prim #1, prim #2.

So it might be best to use a single primitive type through the whole game. Let's not make this the triangle for now :) Raytracing volumes of revolution with the form y^2 = Ar^2 + Br + C is quite easy, and by combining those volumes you can make arbitrary lathed objects. A game with just Wolf 3D walls and lathed objects could be a thing! :)

Conclusion

If you've followed so far, you've probably got as many questions to ask as I've answered.

I first implemented this idea in WebGL, for very simple worlds. I then worked on a DX11 version, but I didn't have time to polish that very much (mouths to feed!)

Obvious open questions are:

• What is the best algorithm and/or heuristic for generating the "tree"
• How much memory is this going to take?
• What about games more sophisticated than Wolf 3D? (well, hey - if rasterized 3D games started there, why can't raytraced 3D games?)

There's lots of possible ideas here - play with heuristics, or think a bit more; reduce memory maybe by using a multi-resolution voxel space (so big areas have fewer texels painted on them, reducing space); and ultimately perhaps make a triangle-based renderer and maybe use SIMD to intersect 4 triangles at once, disallowing nodes with > 4 triangles in them if you can!

I would love to play some more with this but I have other fish to fry. If you try implementing these ideas, do get in touch. And please give me credit if you make the world's first realtime raytraced game based on this algorithm :) I have a feeling that this algorithm makes this possible, just, today. So long as the game is Wolf 3D or Descent or something like that :)

Any questions? :)

Example Code

The example code needs Visual Studio 2008 and the latest DirectX SDK to compile. It's bereft of anything useful like comments, but you can run it and without too much effort you can dig around in VoxelDeconstruction.cpp and render your own voxelized models :) Note that the long startup time is due to the creation of the divs, which is not fast even for small models!

DOWNLOAD EXAMPLE CODE